Estrutura de Dados: computação na prática com Java

Introdução

Imagine administrar uma grande quantidade de dados em seu programa, você com certeza procuraria utilizar a forma mais benéfica e eficiente, porém, como escolher a solução mais viável?

Estrutura de dados é a forma de organizar e guardar dados, ela existe para que determinado dado possa ser utilizado de maneira eficiente, possibilitando uma melhor administração. O objetivo deste artigo é entender como as estruturas de dados funcionam por baixo dos panos, discutir as vantagens e desvantagens de cada uma e ver, em diferentes situações, qual é o tempo de execução e performance dessas estruturas. Esse conhecimento é importante para podermos optar por uma delas em nosso programa, ou seja, escolhendo a solução mais viável. Para isso, vamos ver na prática usando como base um projeto em Java.

Armazenamento sequencial e Vetores

Com o Eclipse aberto, vamos começar o nosso primeiro projeto de estrutura de dados. Como exemplo, estaremos trabalhando com uma universidade, onde precisamos guardar e recuperar dados dos alunos. Ou seja, vamos adicioná-lo no fim ou no meio de uma lista, removê-lo, achá-lo a partir de seu número e assim por diante.

O primeiro passo nesse projeto é modelar a Classe "Aluno". Para isso criamos um novo projeto e dentro dele a classe Aluno, que é onde guardaremos o nome do aluno, que receberemos no próprio Construtor da Classe.

Em seguida, vamos criar o getter e implementar os métodos "equals" e "toString", que serão muito importantes. O "equals" é o método que serve para comparar dois objetos, no caso alunos. Faremos um casting do object para aluno. O "toString" retorna o nome do aluno:

package ed;

public class Aluno {

    private String nome;

    public Aluno(String nome) {
        this.nome = nome;
    }

    public String getNome() {
         return nome;
     }

@Override
public boolean equals(Object obj) {
    Aluno outro = (Aluno) obj;
    return outro.getNome().equals(this.nome);
}

@Override
public String toString() {
    return nome;
 }
}

Ao fazer isso, a primeira estrutura de dados que veremos é o Armazenamento Sequencial. A ideia dessa estrutura é armazenar um aluno atrás do outro. Teremos um conjunto de espaços (Array), sendo que: o primeiro aluno fica no primeiro espaço, o segundo aluno no segundo espaço, e assim por diante.

Sabendo disso, vamos criar uma nova Classe, chamada "Vetor", na qual é preciso implementar a estrutura de armazenamento sequencial. Além disso, precisamos inserir um array com 100 posições e implementar os métodos dos comportamentos desse array:

package ed;

public class Vetor {
 private Aluno[] alunos = new Aluno[100];

    public void adiciona(Aluno aluno) {
        //recebe um aluno
    }

    public Aluno pega(int posicao) {
        //recebe uma posição e devolve o aluno
        return null;
    }

    public void remove(int posicao) {
        //remove pela posição
    }

    public boolean contem(Aluno aluno) {
        //descobre se o aluno está ou não na lista
        return false;
    }

    public int tamanho() {
        //devolve a quantidade de alunos
        return 0;
    }

    public String toString() {
        //facilitará na impressão
        return Arrays.toString(alunos);
    }

}

Os return's já foram inseridos para que possamos compilar o código. Antes de implementar os comportamentos, iremos escrever o método main para testar o Vetor, antes mesmo do código existir. Para isso vamos criar a Classe "VetorTeste":

package ed;

public class VetorTeste {

    public static void main(String[] args) {

    }
}

Método adiciona

O primeiro método que vamos testar é o "adiciona", usando dois alunos:

    public static void main(String[] args) {
        Aluno a1 = new Aluno("Joao");
        Aluno a2 = new Aluno("Jose");

        Vetor lista = new Vetor();

        lista.adiciona(a1);
        lista.adiciona(a2);

        System.out.println(lista);
    }

Ao rodar o programa, ele retorna:

[null, null, null, null, null...]

Serão 100 null's, então o método "adiciona" está funcionando. Então vamos implementá-lo? A ideia é percorrer todo o array e, assim que encontrar uma posição nula, o aluno da vez é armazenado nela:

    public void adiciona(Aluno aluno) {
        for(int i = 0; i < alunos.length; i++) {
            if(alunos[i] == null) {
                alunos[i] = aluno;
                break;
            }
        }
    }

Rodando novamente o teste, ele vai retornar:

[Joao, Jose, null, null, null...]

Agora os dois alunos foram inseridos no array. Mas perceba que o algoritmo que implementamos não é muito performático, pois quanto maior o número de alunos inseridos no array, mais demorado será o método, uma vez que o laço irá percorrer várias vezes os espaços já preenchidos. Vamos tentar melhorá-lo para que não fique dependente da quantidade de elementos na lista. Para isso, vamos usar do seguinte código:

    private Aluno[] alunos = new Aluno[100];
    private int totalDeAlunos = 0;

    public void adiciona(Aluno aluno) {
        this.alunos[totalDeAlunos] = aluno;
        totalDeAlunos++;
    }

Método tamanho

O próximo método que vamos testar é o "tamanho":

    public int tamanho() {
        return totalDeAlunos;
    }

Vamos acrescentar no método main:

        System.out.println(lista.tamanho());
        lista.adiciona(a1);
        System.out.println(lista.tamanho());
        lista.adiciona(a2);
        System.out.println(lista.tamanho());

Ele retornará:

0
1
2
[Joao, Jose, null, null, null...]

A cada iteração ele retorna o tamanho da lista de alunos preenchida.

Método contem

Vamos implementar o método "contem". Queremos "perguntar" para a lista se um aluno específico está ou não nela.

    public boolean contem(Aluno aluno) {

        for(int i = 0; i < totalDeAlunos; i++) {
            if(aluno.equals(alunos[i])) {
                return true;
            }
        }
        return false;
    }

Para testar o "true", adicionamos no *main:

System.out.println(lista.contem(a1));

Rodando:

0
1
2
[Joao, Jose, null, null, null...]
true

Para testar o "false" criamos um aluno que não será adicionado na lista:

Aluno a3 = new Aluno("Danilo");
System.out.println(lista.contem(a3));

Rodando:

0
1
2
[Joao, Jose, null, null, null...]
true
false

Método pega

Para implementar este método - que nos retorna o nome do aluno na posição que perguntamos - fazemos:

    public Aluno pega(int posicao) {
        return alunos[posicao];
    }

Lembre-se que nosso array possui 100 posições. O que aconteceria se perguntássemos sobre o aluno na posição 200? Vamos testar pelo main:

Aluno x = lista.pega(1);
System.out.println(x);

O programa retorna o "Jose", pois é ele que está na posição de número 1. Se escolhermos a posição 200, o programa retorna um erro com a mensagem "ArrayIndexOutOfBounds", ou seja, estamos tentando acessar uma posição do array que não existe.

Vamos começar a pensar na validação dos dados que vamos passar para o programa. Precisamos que ele retorne, por exemplo, uma mensagem mais amigável, ao invés de um erro. Criaremos um método auxiliar que irá dizer se uma determinada posição está ocupada ou não:

private boolean posicaoOcupada(int posicao) {
    return posicao >= 0 && posicao < totalDeAlunos;
}

No método "pega":

    public Aluno pega(int posicao) {

        if(!posicaoOcupada(posicao)) {
            throw new IllegalArgumentException("posiçao invalida");
        }

        return alunos[posicao];
    }

Essa parte é muito importante, pois é nossa responsabilidade a implementação da estrutura para garantir que ela trate bem qualquer dado errado passado pelo usuário.

Outro método adiciona

Vamos implementar um outro método que, diferentemente do "adiciona" que já vimos, insere um aluno em qualquer posição do array:

public void adiciona(int posicao, Aluno aluno) {

}

Vamos pensar como construir esse método. Vamos imaginar, no nosso array de 100, que as primeiras dez posições já estão preenchidas. Queremos inserir um aluno na terceira posição, como na imagem abaixo:

Imagem de fundo azul escuro, com nove retângulos verticais na cor cinza e enfileirados horizontalmente. O terceiro retângulo está destacado pela cor vermelha.

Para isso, vamos arrastar todos os alunos da terceira posição em diante para a direita e colocamos aquele aluno no buraco que ficou, como podemos observar na imagem a seguir:

Imagem de fundo azul escuro, com cinco retângulos verticais enfileirados horizontalmente, onde a terceira posição está vazia e a quarta posição é ocupada por um retângulo destacado pela cor vermelha.

Então fazemos:

public void adiciona(int posicao, Aluno aluno) {

    for(int i = totalDeAlunos - 1; i >= posicao; i-=1) {
        alunos[i+1] = alunos[i];
    }
    alunos[posicao] = aluno;
    totalDeAlunos++;
}

Vamos testá-lo adicionando um aluno:

lista.adiciona(1, a3);
System.out.println(lista);

Ao que o programa retorna:

[Jose, Danilo, Jose, null, null...]

O aluno Danilo foi para a posição 1 empurrando todos para a direita. Porém, da mesma forma que o "pega", precisamos de uma validação:

private boolean posicaoValida(int posicao) {
    return posicao >= 0 && posicao <= totalDeAlunos;
}

E no método:

public void adiciona(int posicao, Aluno aluno) {

    if(!posicaoValida(posicao)) {
        throw new IllegalArgumentException("posicao invalida");
    }
    for(int i = totalDeAlunos - 1; i >= posicao; i-=1) {
        alunos[i+1] = alunos[i];
    }
    alunos[posicao] = aluno;
    totalDeAlunos++;
}

Método remove

O nosso próximo desafio é o método "remove", que será parecido com o "adiciona", porém pensando inversamente: retiramos o aluno da posição n e empurramos para a esquerda todos aqueles que vinham depois dele:

public void remove(int posicao) {
    for(int i = posicao; i < this.totalDeAlunos; i++) {
        this.alunos[i] = this.alunos[i+1];
    }
    totalDeAlunos--;
}

Testando:

lista.remove(1);
System.out.println(lista);

Antes estava assim:

[Jose, Danilo, Jose, null, null...]

E agora:

[Joao, Jose, null, null, null...]

Redimensionando o array

Já implementamos os principais métodos do nosso Vetor. Porém, perceba que o tamanho do array é constante, valendo 100. Nós queremos que ele seja mutável de acordo com o número de alunos.

Em Java não conseguimos mudar o tamanho de um array, então teremos que criar um novo maior e copiar tudo que está no antigo para este. Criamos o método "garanteEspaço":

private void garanteEspaco() {
    if(totalDeAlunos == alunos.length) {
        Aluno[] novoArray = new Aluno[alunos.length*2];
        for(int i = 0; i < alunos.length; i++) {
            novoArray[i] = alunos[i];
        }
        this.alunos= novoArray;
    }

}

Falta agora invocar nos dois métodos "adiciona":

public void adiciona(Aluno aluno) {
    this.garanteEspaco();
    ...
}

public void adiciona(int posicao, Aluno aluno) {
    this.garanteEspaco();
    ...
}

Agora se adicionar mais elementos do que o tamanho do antigo array, ele será redimensionado em um novo array.

Para testar essa implementação vamos criar um laço no main que vai adicionar 300 alunos:

for(int i = 0; i < 300; i++) {
    Aluno y = new Aluno("Joao" + i);
    lista.adiciona(y);
}
System.out.println(lista);

O programa, de fato, retornará uma lista de 300 elementos:

[Joao, Jose, Joao 0, Joao 1, Joao 2, Joao 3...]

Nesse exemplo, perceba que houve dois redimensionamentos:

Quando passou de 100, dobrando o array para 200 posições;
Quando passou de 200, dobrando o array para 400 posições (tendo 100 delas valores null).

O ArrayList

O Java já tem uma implementação de Vetor, é a classe conhecida por "ArrayList". Ela é bem parecida com tudo o que fizemos até agora e funciona como um armazenamento sequencial, possuindo os métodos implementados nesta aula:

ArrayList<Aluno> listaDoJava = new ArrayList<Aluno>();

Apesar dela existir e facilitar nossa vida, foi importante aprendermos como e o que implementar para criarmos uma estrutura de dados.

Listas ligadas

Utilizamos vetores e vimos que são boas estruturas de dados para diversos casos, como: adicionar elementos no fim do vetor; pegar um elemento aleatório; remover elementos.

Porém, outros métodos já não eram tão simples como, por exemplo, inserir um elemento no meio do vetor, esta que é uma atividade computacionalmente cara e com processo de execução lento.

Já vimos o Vetor e observamos seus prós e contras e agora vamos aprender sobre uma outra lista. Com ela tentaremos melhorar o código para que essa adição de elementos no meio do array seja um processo mais rápido.

A essa lista nós damos o nome de lista ligada. A diferença dela para o Vetor é que neste os elementos estão um do lado do outro na memória, enquanto que na lista ligada eles estão em lugares diferentes, porém um aponta para o outro indicando o próximo.

Imagem de fundo azul escuro, com três arquivos representados por um retângulo vertical na cor cinza e enfileirados horizontalmente. Embaixo, a imagem apresenta duas setas brancas: a primeira seta está ligando o primeiro arquivo com o segundo, e a segunda seta está ligando o segundo arquivo com o terceiro.

Então, é dessa forma que iremos desenhar a estrutura, na qual um elemento também conhecerá o endereço do próximo. Para isso, vamos criar uma Classe "Celula" que possuirá um objeto e seu seguinte (do tipo "Celula"). Para facilitar, vamos também criar um Construtor e getters (para o elemento) e setters (para o elemento e para a Celula):

public Celula(Object elemento, Celula proximo) {
    this.elemento = elemento;
    this.proximo = proximo;
}

public Celula getProximo() {
    return proximo;
}

public void setProximo(Celula proximo) {
    this.proximo = proximo;
}

public Object getElemento() {
    return elemento;
}

Agora vamos criar a Classe "ListaLigada" e definir suas funções:

package ed.listaligada;

public class ListaLigada {

    public void adicionaNoComeco(Object elemento) {}

    public void adiciona(Object elemento) {}

    public void adiciona(int posicao, Object elemento) {}

    public Object pega(int posicao) { return null; }

    public void remove(int posicao) {}

    public int tamanho() { return 0; }

    public boolean contem(Object o) { return false;}
}

Método adicionaNoComeco

Vamos começar imaginando que já temos uma lista com células apontando uma para outra. Para uma nova Célula entrar no começo do array ela deve apontar para sua próxima, ou seja, a primeira do array atual. Então devemos ter um atributo chamado "primeira". Como a lista começa vazia, essa célula aponta para null:

public class ListaLigada {

    private Celula primeira = null;

    public void adicionaNoComeco(Object elemento) {
        Celula nova = new Celula(elemento, primeira);

    }

Na lista vazia, ao adicionarmos uma célula na primeira posição do array, ela deverá apontar para null. Já quando acrescentamos uma próxima, também no começo, esta apontará para a anterior; e soma-se 1 ao total de elementos:

public class ListaLigada {

    private Celula primeira = null;
    private int totalDeElementos = 0;

    public void adicionaNoComeco(Object elemento) {
        Celula nova = new Celula(elemento, primeira);
        this.primeira = nova;

        this.totalDeElementos++;
    }

Para testar, vamos criar a Classe "TestaListaLigada" com o método main e implementar para imprimir depois de cada inserção de elemento:

package ed.listaligada

public class TestaListaLigada {

    public static void main(String[] args) {
        ListaLigada lista = new ListaLigada();

        System.out.println(lista);
        lista.adicionaNoComeco("mauricio");
        System.out.println(lista);
        lista.adicionaNoComeco("paulo");
        System.out.println(lista);
        lista.adicionaNoComeco("guilherme");
        System.out.println(lista);
    }
}

Se deixarmos desse jeito, o retorno não será amigável e não entenderemos nada. Vamos criar um toString amigável na Classe "ListaLigada":

@Override
public String toString () {

    if(this.totalDeElementos == 0) {
        return "[]";
    }

    Celula atual = primeira;

    StringBuilder builder = new StringBuilder("[");

    for(int i = 0; i < totalDeElementos; i++) {
        builder.append(atual.getElemento());
        builder.append(",");

        atual = atual.getProximo();
    }

    builder.append("]");

    return builder.toString();
}

Ao rodarmos, retorna:

[]
[mauricio,]
[paulo,mauricio,]
[guilherme,paulo,mauricio,]

Método adiciona (no fim da lista)

Para Listas Ligadas, este método é um pouco mais complexo. O que nos diz se um elemento é o último do array é se ele apontar para um null. Para isso é necessário varrer toda a lista. Vamos resolver o problema criando uma seta para o último elemento (da mesma forma que fizemos para o primeiro):

private Celula primeira = null;

private Celula ultima = null;

Com essa mudança teremos que arrumar algumas coisas no método "adicionaNoComeco". Se a lista está vazia, o primeiro elemento também será o último:

    public void adicionaNoComeco(Object elemento) {
        Celula nova = new Celula(elemento, primeira);
        this.primeira = nova;

        if(this.totalDeElementos == 0) {
            this.ultima = this.primeira;
        }

        this.totalDeElementos++;
    }

Voltemos ao desafio de inserir no final. Criamos uma nova célula cujo próximo elemento é null, afinal ela está sendo adicionada no final do array. Precisamos fazer com que a última atual aponte para essa nova.

public void adiciona(Object elemento) {

    Celula nova = new Celula(elemento, null);
    this.ultima.setProximo(nova);
    this.ultima = nova;
    this.totalDeElementos++;    
}

Mas precisamos cuidar do caso particular em que a lista está vazia e faremos isso nos utilizando do outro método já implementado:

public void adiciona(Object elemento) {

    if(this.totalDeElementos == 0) {
        adicionaNoComeco(elemento);
    } else {
        Celula nova = new Celula(elemento, null);
        this.ultima.setProximo(nova);
        this.ultima = nova;
        this.totalDeElementos++;
    }
}

Vamos testar:

lista.adiciona("marcelo");
System.out.println(lista);

O que retorna:

[guilherme,paulo,mauricio,marcelo,]

Método adiciona (no meio da lista)

Para implementarmos esse método vamos criar outros dois para ajudar. Um irá indicar quando a posição existir, estiver ocupada:

private boolean posicaoOcupada(int posicao) {
    return posicao >= 0 && posicao < this.totalDeElementos;
}

E o outro irá apontar para a célula na qual queremos inserir o elemento:

private Celula pegaCelula(int posicao) {

    if(!posicaoOcupada(posicao)) {
        throw new IllegalArgumentException("posicao inexistente");
    }

    Celula atual = primeira;

    for(int i = 0; i < posicao; i++) {
        atual = atual.getProximo();
    }
    return atual;
}

Imaginemos agora, mais uma vez, que já possuímos uma lista onde um elemento aponta para o outro. O elemento da esquerda deve apontar para o novo, e este para o da direita. Então, em código, fazemos:

public void adiciona(int posicao, Object elemento) {

    Celula anterior = this.pegaCelula(posicao - 1);
    Celula nova = new Celula(elemento, anterior.getProximo();
}

Dessa forma pegamos a Célula da esquerda (anterior) e a nova no lugar da próxima (anterior.getProximo). Por fim, basta fazer com que a anterior seja a nova e somar 1 no total de elementos:

public void adiciona(int posicao, Object elemento) {

    Celula anterior = this.pegaCelula(posicao - 1);
    Celula nova = new Celula(elemento, anterior.getProximo());
    anterior.setProximo(nova);
    this.totalDeElementos++;
}

Ainda falta implementar o método para quando a lista estiver vazia ou quando a posição "do meio" seja, na realidade, a última:

public void adiciona(int posicao, Object elemento) {

    if(posicao == 0) {
        adicionaNoComeco(elemento);
    } else if (posicao == this.totalDeElementos) {
        adiciona(elemento);
    } else {
        Celula anterior = this.pegaCelula(posicao - 1);
        Celula nova = new Celula(elemento, anterior.getProximo();
        anterior.setProximo(nova);
        this.totalDeElementos++;
}

Vamos testar, fazendo no main:

lista.adiciona(2, "gabriel");
System.out.println(lista);

O que retorna:

[guilherme,paulo,gabriel,mauricio,marcelo,]

Método pega

Para o "pega":

public Object pega(int posicao) {
    return this.pegaCelula(posicao).getElemento();
}

No main:

Object x = lista.pega(2);
System.out.println(x);

Retorna:

gabriel

Método tamanho

Para o "tamanho":

public int tamanho() {
    return this.totalDeElementos;
}

No main:

System.out.println(lista.tamanho());

O que retorna:

Método remove

Antes de implementarmos o método "remove", vamos fazer o "removeDoComeco":

public void removeDoComeco() {
    if(this.totalDeElementos == 0) {
        throw new IllegalArgumentException("lista vazia");
    }

    this.primeira = this.primeira.getProximo();
    this.totalDeElementos--;

    if(this.totalDeElementos == 0) {
        this.ultima = null;
    }
}

Testando:

lista.removeDoComeco();
System.out.println(lista);

O que retorna:

[paulo,gabriel,mauricio,marcelo]

O elemento na primeira posição (Guilherme) foi removido.

Listas duplamente ligadas

Já aprendemos sobre Listas ligadas, cuja ideia era a de que uma célula estava ligada à sua próxima em um array. Ela nos facilitou em relação à implementação e velocidade de execução.

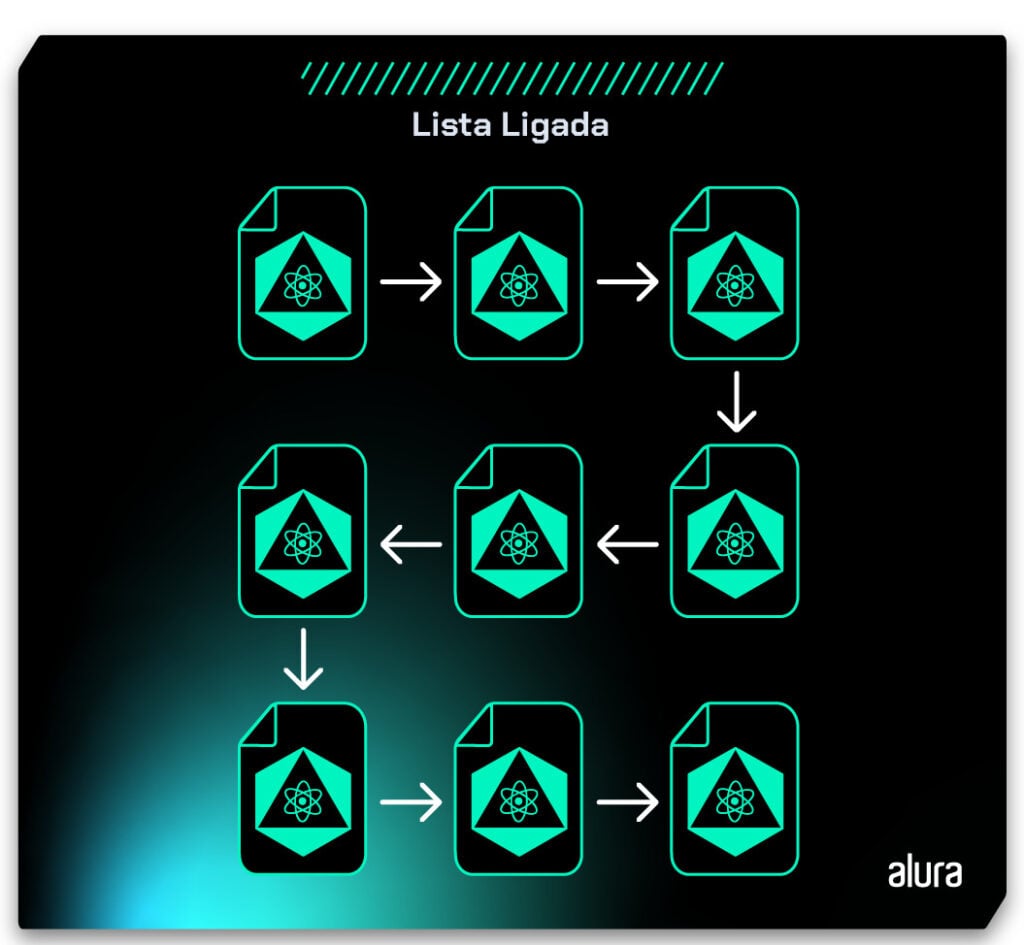
Esquema, em fundo azul, exibindo nove arquivos organizados em três linhas diferentes, distribuindo três arquivos em cada linha. Cada arquivo se conecta por meio de uma seta de forma sequenciada. Ao término de cada linha, o último arquivo se conecta ao próximo arquivo posicionado abaixo, retomando a sequência de conexões e repetindo o padrão de ligações até a chegada ao último arquivo da terceira linha.

Agora, vamos conhecer as Listas duplamente ligadas, cujos elementos não apenas apontam para seu próximo, mas também para seu anterior.

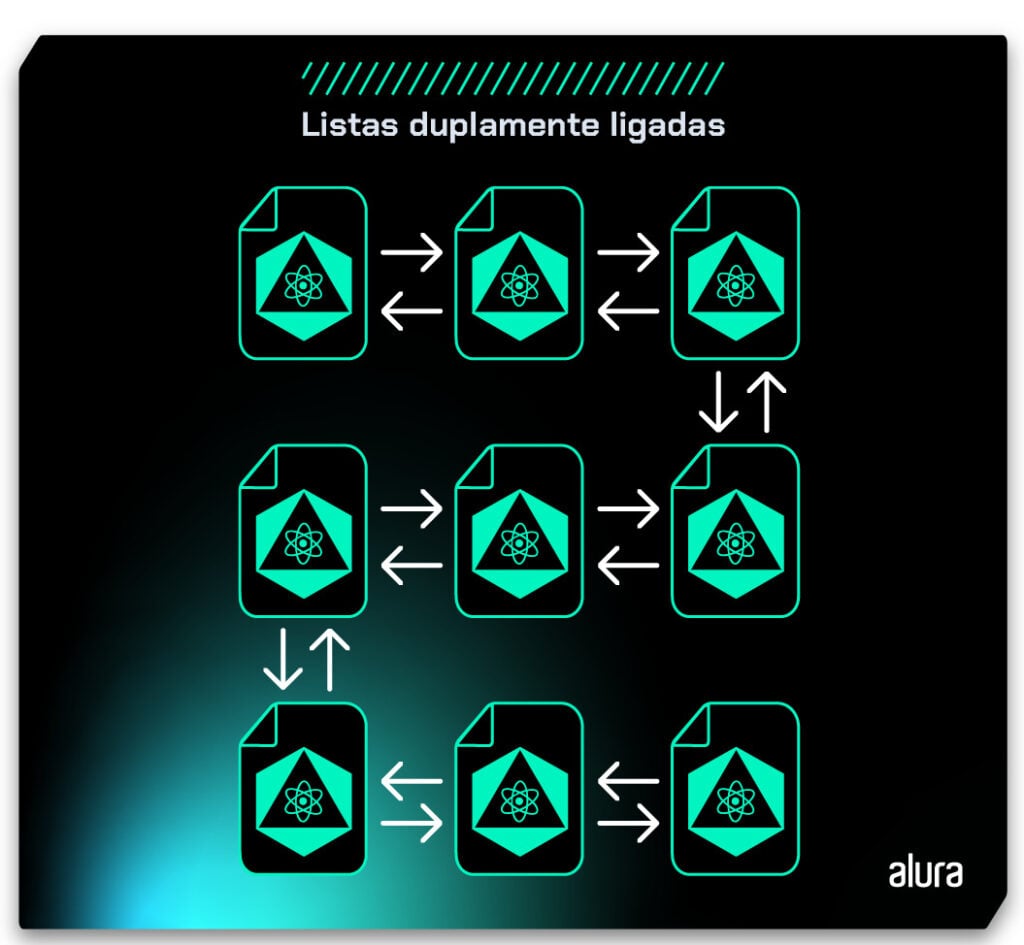
Então, voltando à nossa Classe Celula, vamos criar um novo parâmetro com seu getter e setter:

private Celula anterior;

...

public Celula getAnterior() {
    return anterior;
}

public void setAnterior(Celula anterior) {
    this.anterior = anterior;
}

E vamos criar um Construtor que irá nos ajudar ao implementarmos o primeiro método:

public Celula(Object elemento) {
    this(null, elemento);
}

Vamos, a partir de agora, repensar o nosso código implementado na aula anterior para ele se adequar aos novos parâmetros.

Método adicionaNoComeco

Na Classe "ListaLigada", o primeiro método que implementamos foi o "adicionaNoComeco". Vamos reescrevê-lo:

public void adicionaNoComeco(Object elemento) {
    if(this.totalDeElementos == 0) {
        Celula nova = new Celula(elemento);
        this.primeira = nova;
        this.ultima = nova;
    } else {
        Celula nova = new Celula(this.primeira, elemento);
        this.primeira.setAnterior(nova);
        this.primeira = nova;
    }
    this.totalDeElementos++;
}

Vamos entender este código:

Se a lista está vazia, criamos uma célula e o próximo dela é null e logicamente o anterior também. Isto já havíamos feito anteriormente;
Criamos uma nova célula cuja próxima é a primeira. E a anterior a esta é a nova. E a primeira é a nova.

Método adiciona (no fim)

public void adiciona(Object elemento) {
    if(this.totalDeElementos == 0) {
        adicionaNoComeco(elemento);
    } else {
        Celula nova = new Celula(elemento);
        this.ultima.setProxima(nova);
        nova.setAnterior(this.ultima);
        this.ultima = nova;
        this.totalDeElementos++;

Muito parecido com o método anteriormente implementado. A única diferença é que setamos para a célula anterior.

Vamos relembrar o que fizemos?

Criamos uma nova célula.
A última aponta a próxima para essa nova célula.
A nova aponta a anterior para a última atual.
A última atual agora é a nova célula.

Método adiciona (numa posição qualquer)

public void adiciona(int posicao, Object elemento) {

    if(posicao == 0) {
        adicionaNoComeco(elemento);
    } else if (posicao == this.totalDeElementos) {
        this.adiciona(elemento);
    } else {
        Celula anterior = pegaCelula(posicao - 1);
        Celula proxima = anterior.getProxima();

        Celula nova = new Celula(anterior.getProxima(), elemento);
        nova.setAnterior(anterior);
        anterior.setProxima(nova);
        proxima.setAnterior(nova);
        this.totalDeElementos++;
}

Método remove (do fim)

Agora que sabemos sobre lista duplamente ligada, podemos fazer o método remove do fim.

Se o array possui apenas um elemento, chamamos o método "removeDoComeco":

public void removeDoFim() {
    if(this.totalDeElementos == 1) {
        this.removeDoComeco();
    }

Para removermos o elemento do fim, precisamos da penúltima célula, que está ligada a ele:

public void removeDoFim() {
    if(this.totalDeElementos == 1) {
        this.removeDoComeco();
    } else {
        Celula penultima = this.ultima.getAnterior();
        penultima.setProxima(null);
        this.ultima = penultima;
        this.totalDeElementos--;
    }
}

Vamos testar o método. Antes, a lista possuía mauricio, cecilia, paulo. Chamando a função:

lista.removeDofim();
System.out.println(lista);

O retorno será:

[mauricio, cecilia]

Método remove (de qualquer posição)

Se o elemento estiver na primeira ou na última posição basta chamar os métodos já implementados:

public void remove(int posicao) {
    if(posicao == 0) {
        this.removeDoComeco();
    } else if (posicao == this.totalDeElementos - 1) {
        this.removeDoFim();
    }
}

Mas agora precisamos pensar em como remover o elemento do meio. Vamos navegar e dar os nomes aos elementos e setar seus anteriores e próximos:

public void remove(int posicao) {
    if(posicao == 0) {
        this.removeDoComeco();
    } else if (posicao == this.totalDeElementos - 1) {
        this.removeDoFim();
    } else {
        Celula anterior = this.pegaCelula(posicao - 1);
        Celula atual = anterior.getProximo();
        Celula proxima = atual.getProximo();

        anterior.setProximo(proxima);
        proxima.setAnterior(anterior);

        this.totalDeElementos--;
    }
}

Vamos testar este método. Primeiramente acrescentamos mais alguns nomes na lista para termos algo assim:

[mauricio, cecilia, jose, joao]

Agora fazemos, por exemplo:

lista.remove(2);
System.out.println(lista);

O que nos retorna:

[mauricio, cecilia, joao]

O elemento na posição 2, José, foi removido da lista.

Método contem

Este método será parecido com o do Vetor. Vamos utilizar o while, que é uma outra abordagem de laço.

public boolean contem(Object elemento) {
    Celula atual = this.primeira;

    while(atual != null) {
        if(atual.getElemento().equals(elemento)) {
            return true;
        }
        atual = atual.getProximo();
    }
    return false;
}

O método varrerá todo o array até encontrar, (true) ou não (false), o elemento citado.

Vamos testar:

System.out.println(lista.contem("mauricio"));
System.out.println(lista.contem("danilo"));

O programa retornará:

true
false

O Maurício está na lista e o Danilo não.

Pilhas

Já aprendemos sobre listas ligadas e duplamente ligadas. Tais listas possuíam células que apontavam para outras, anteriores e posteriores. Vimos nos exercícios que o Java já tem tudo isso implementado por meio da Classe LinkedList.

Neste momento, veremos uma outra estrutura de dados cuja principal diferença, em relação aos outros tipos de estruturas de dados, é guardar os diversos estados de uma aplicação para que no futuro, se necessário, seja possível voltar a estes estados. A essa estrutura damos o nome de Pilha.

Vamos criar um pacote e, dentro dele, a Classe "Pilha". As operações que teremos nessa pilha são:

package ed.pilha

public class Pilha {

    public void insere(String nome) {

    }

    public String remove() {
        return "";
    }

    public boolean vazia() {
        return false;
    }
}

A Pilha segue a regra de inserção de elementos um após o outro e a remoção funciona da mesma forma, do último para o primeiro elemento. Para começar a implementar, não começamos do zero. Já temos uma parte do código feita, pois a fizemos nos estudos de listas. Vamos utilizar a implementação que o Java nos oferece.

package ed.pilha

import java.util.LinkedList;
import java.util.List;

public class Pilha {

private List<String> nomes = new LinkedList<String>();

Vamos criar um documento para teste para começar a implementar os métodos:

package ed.pilha

public class TesteDaPilha {

    public static void main(String[] args) {
        Pilha pilha = new Pilha();
    }
}

O que já devemos implementar também é o toString:

@Override
public String toString() {
    return nomes.toString();
}

Método insere

Implementar o método utilizando o conceito de Pilha é simples, pois sempre seguiremos uma ordem. Então o método insere ficará assim:

public void insere(String nome) {
    nomes.add(nome);    
}

Testando:

pilha.insere("Mauricio");
System.out.println(pilha);

pilha.insere("Guilherme");
System.out.println(pilha);

O que retorna:

[Mauricio]
[Mauricio, Guilherme]

Método remove

Aqui basta chamar o "remove" do LinkedList passando o elemento na casa nomes.size()-1:

public String remove() {
    return nomes.remove(nomes.size()-1);
}

Para testar vamos pedir para imprimir cada elemento que será removido e depois a lista final:

String r1 = pilha.remove();
System.out.println(r1);

String r2 = pilha.remove();
System.out.println(r2);

System.out.println(pilha);

O que nos retorna:

Guilherme
Mauricio
[]

Os elementos foram removidos começando do final da lista.

Método vazia

Este método indica se a lista está vazia ou não. Temos duas maneiras de implementá-lo:

public boolean vazia() {
    return nomes.size() == 0;
}

Ou usando a função do LinkedList:

public boolean vazia() {
    return nomes.isEmpty();
}

Para testar, vamos imprimir o comando booleano System.out.println(pilha.vazia()); antes e depois de inserir elementos na lista. Veremos que retornará:

true
false

Antes a lista estava vazia e após inserirmos os elementos ela não estará mais.

O Java também já possui uma Classe própria para pilhas, cujo nome é Stack. Substituindo os nomes de nossos métodos para os da Classe do Java, temos:

insere -> push
remove -> pop

Podemos escrever no arquivo de teste:

Stack<String> stack = new Stack<String>();
stack.push("Mauricio");
stack.push("Marcelo");

System.out.println(stack);

O que imprime [Mauricio, Marcelo]. E para remover:

stack.pop();
System.out.println(stack);

O quê imprime [Mauricio].

Método peek

Como vimos, o pop remove o último elemento da pilha. O método peek trabalha em cima desse elemento também, porém sem removê-lo, já que ele apenas o retorna. Portanto, se temos a pilha [Mauricio, Marcelo],

String nome = stack.peek();
System.out.println(nome);

Nos retorna Marcelo.

Usabilidade das pilhas

O conceito de pilhas é amplamente utilizado por compiladores e autômatos, portanto, podemos afirmar que essa estrutura de dados tem muita usabilidade em ciência da computação. O próprio, e muito conhecido, comando "Desfazer" dos editores de texto, de código, de imagens, etc. tem como base as pilhas. Podemos também brincar com palavras e inverter a ordem de suas letras utilizando as pilhas.

Filas

Agora vamos conhecer as Filas, que se estruturam de modo parecido com as pilhas. Porém, diferente das pilhas, na qual o primeiro elemento a entrar é o último a sair, em filas o primeiro a entrar é o primeiro a sair.

Criemos a Classe "Fila", que será suportada pelo LinkedList, e terá alguns métodos e o toString.

package ed.fila;

import java.util.LinkedList;
import java.util.List;

public class Fila {

    private List<String> alunos = new LinkedList<String>();

    //métodos

@Override
public String toString() {
    return alunos.toString();
}

}

Criamos também, como é de costume, o método main para testar as funções de Fila:

package ed.fila

public class TesteDaFila {

    public static void main(String[] args) {
        Fila fila = new Fila();

    }
}

Método adiciona

Este método funciona igual ao da Pilha:

public void adiciona(String aluno) {
    alunos.add(aluno);
}

Fazemos para teste:

fila.adiciona("Mauricio");
fila.adiciona("Guilherme");

System.out.println(fila);

O quê retorna:

[Mauricio, Guilherme]

Método remove

Lembre-se que, na estrutura de Fila, será removido sempre o primeiro elemento do array, então fazemos:

public String remove() {
    return alunos.remove(0);
}

Para testarmos:

String x1 = fila.remove();
System.out.println(x1);
System.out.println(fila);

O que retorna:

Mauricio
[Guilherme]

"Mauricio", que é o primeiro elemento, foi removido.

Método vazia

Nos falta ainda esse método. Implementamos da seguinte forma:

public boolean vazia() {
    return alunos.isEmpty();
}

Queue

Da mesma forma que a estrutura de Pilhas tinha o nome de Stack, à estrutura de Filas damos o nome de Queue:

Queue<String> filaDoJava = new LinkedList<String>();

Para as filas os métodos têm os seguintes nomes:

adiciona: add
remove: poll

Implementamos da seguinte forma:

Queue<String> filaDoJava = new LinkedList<String>();

filaDoJava.add("Mauricio");
String x2 = filaDoJava.poll();

Se imprimirmos o x2, nos retorna Mauricio.

Conclusão

Neste artigo, vimos na prática vetores, lista ligada, lista duplamente ligada, pilha e fila. É muito importante compreender como uma estrutura funciona por baixo dos panos e, por isso, o estudo de estrutura de dados é uma parte fundamental na programação e na formação de profissionais da área. Aprendendo isso, você estará preparado para optar pela melhor solução.

Se esse conteúdo te interessou, você pode acessar os links abaixo para potencializar sua aprendizagem:

Esse artigo é baseado em um conteúdo desenvolvido pelo Maurício Aniche, em 2014.

Estrutura de Dados: computação na prática com Java

Introdução

Armazenamento sequencial e Vetores

Método adiciona

Método tamanho

Método contem

Método pega

Outro método adiciona

Método remove

Redimensionando o array

O ArrayList

Listas ligadas

Método adicionaNoComeco

Método adiciona (no fim da lista)

Método adiciona (no meio da lista)

Método pega

Método tamanho

Método remove

Listas duplamente ligadas

Método adicionaNoComeco

Método adiciona (no fim)

Método adiciona (numa posição qualquer)

Método remove (do fim)

Método remove (de qualquer posição)

Método contem

Pilhas

Método insere

Método remove

Método vazia

Método peek

Usabilidade das pilhas

Filas

Método adiciona

Método remove

Método vazia

Queue

Conclusão

Cursos