Modelos matemáticos utilizados em séries temporais

Em problemas de previsão em séries temporais, comumente, ajustamos curvas aos dados observados. O intuito disso é que ao ajustar essa curva obtemos os coeficientes da equação da curva, tornando possível o cálculo de valores que estão fora do intervalo dos dados observados.

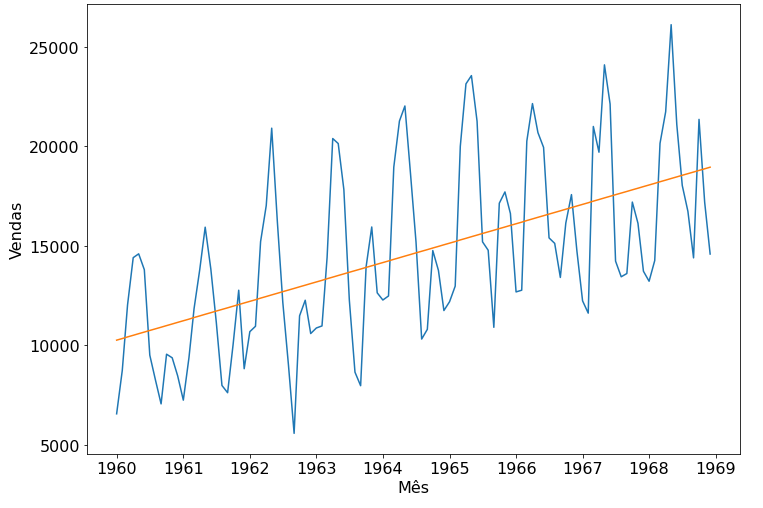
Aqui, nós temos um exemplo de série temporal onde foi ajustada uma reta. Para ajustar essa reta, tivemos que estimar os coeficientes a e b da equação da reta.

Exemplo de série temporal de vendas de carros na década de 1960 com ajustada aos dados

A equação da reta pode ser escrita de forma genérica como:

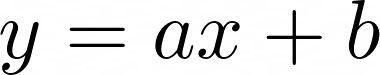
(1) Equação da reta; y = ax +b

Em nosso exemplo, queremos calcular o número de carros vendidos em um determinado mês. Ajustando uma reta à esses dados temos a possibilidade de inserir o valor de mês na equação e obter o número de carros vendidos como resultado. Neste caso, a equação da reta toma esta forma:

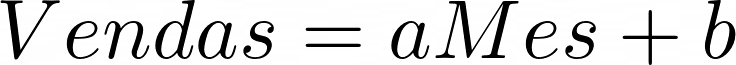
(2) Equação da reta modificada; Vendas = aMes +b

Conhecendo esses coeficientes, podemos calcular qualquer ponto da reta, até os de 1970 em diante. É nesse ponto em que estamos fazendo uma previsão. Mas qual equação temos que ajustar no caso desta figura?

Exemplo de série temporal com caráter semelhante ao de um sinal aleatório

Modelos autorregressivos e de média móvel

A escolha de uma equação que ajusta uma série temporal sem o conhecimento prévio do problema é extremamente difícil. Neste caso, podemos pensar que queremos estimar o próximo ponto na série temporal e que existe uma dependência linear no tempo entre as amostras. Desta forma, podemos estimar o ponto seguinte y_t através do conhecimento de um ponto anterior y_{t-1}.

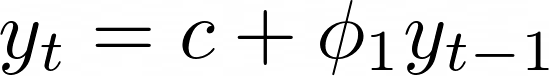
(3) $Modelo autorregressivo de ordem 1. y_t = c + phi y_{t-1}$

A equação 3 é um exemplo de modelo autorregressivo. Nela, o c é uma constante e phi_1 é o coeficiente que devemos determinar para estabelecer uma relação entre o y_t e o y_{t-1}. Porém, a estimativa de y_t pode depender de mais pontos da série temporal.

Imagem que a cada x segundos você observa um evento com uma forma característica, um evento sazonal, por exemplo. Neste caso, precisamos de uma versão generalizada da equação 3 que considere p pontos anteriores da série temporal. A equação a seguir cumpre este papel.

(4)
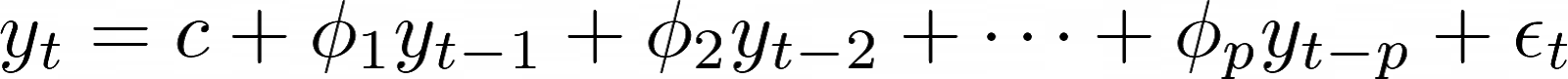
$Modelo autorregressivo de ordem p. y_t = c + \phi_1y_{t-1} + \phi_2y_{t-2} + \dots +\phi_py_{t-p} + \epsilon_t$

Na equação (4) o épsilon representa o ruído aleatório que pode estar presente nos nossos dados. A equação 4 recebe o nome de modelo autorregressivo.

Mas existem outros tipos de modelos que podem ser ajustados a uma série temporal. Outro exemplo de modelo é o de média móvel. Este tipo de modelo é escrito na seguinte forma:

. (5)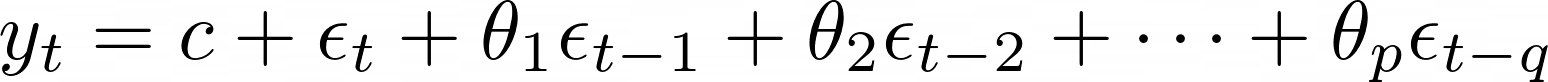
$Modelo de média móvel de ordem q.y_t = c + \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \dots + \theta_p \epsilon_{t-q}$

Repare que na equação 5 os termos theta_q são os coeficientes que queremos encontrar e os termos épsilon representam as amostras de ruído aleatório. Ou seja, estamos procurando os coeficientes que fazem com que o ruído aleatório adquira as características dos nossos dados.

Da combinação dos modelos autorregressivos e de média móvel, temos modelos ARMA. A determinação da ordem p e q desses modelos pode ser feita através da análise das funções de autocorrelação e autocorrelação parcial. Uma alternativa é a utilização de algoritmos que realizam uma busca, ajustando modelos de ordens diferentes na série temporal, como a função AutoArima da biblioteca pmdarima.

Estacionariedade

Os modelos ARMA precisam que a série temporal seja estacionária para serem aplicados. Ou seja, eles precisam que a série temporal não possua tendência ou sazonalidade. Quando a série não é estacionária, aplicamos modelos ARIMA. O ‘I’ do ARIMA está ligado a um processo que permite transformar uma série temporal não estacionária em uma série estacionaria. Terminado esse processo, é adotado um modelo ARMA para a previsão. .

Facebook Prophet

Porém, existe uma alternativa quando a série não é estacionária. Esta alternativa é a aplicação de um modelo que ajusta a série, considerando características não estacionárias como tendência e sazonalidade.

O modelo ajustado pelo FBProphet é do tipo:

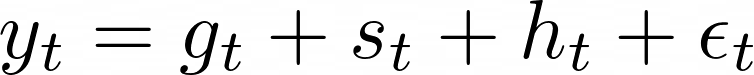
(6) $Modelo assumido pelo Facebook Prophet. y_t = g_t + s_t + h_t + \epsilon_t$

Neste caso, a série usa o termo g para modelar a tendência, o s para as mudanças periódicas e o h para efeitos específicos, como: feriados. A tendência pode ser modelada como uma equação de reta (1). Já, a parte sazonal, utiliza série de Fourier:

. (7) 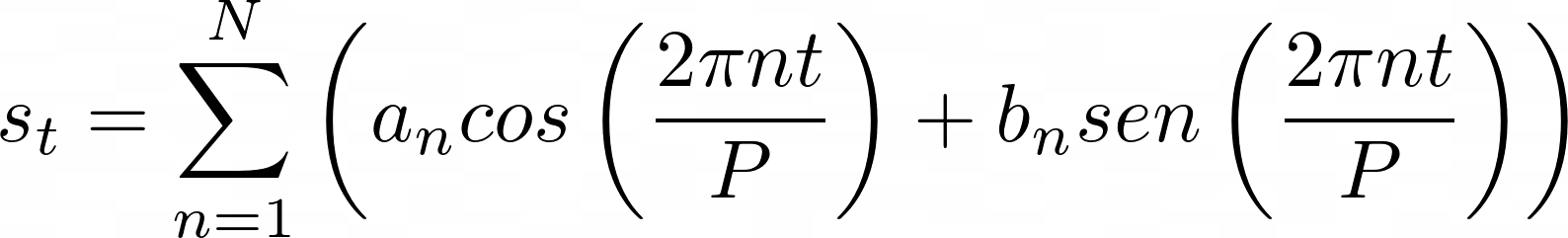$Exemplo de série de Fourier. s_t = \sum_{n=1}^N \left(a_n cos \left( \frac{2 \pi n t}{P} \right) +b_n sen \left( \frac{2 \pi n t}{P} \right) \right)$

Em (7) P é igual a 365,25 no caso de sazonalidade anual. Se as séries de Fourier não são familiares para você, repare que elas são uma combinação de funções seno e cosseno. Funções seno e cosseno, mais ou menos, apertadas conseguem modelar os efeitos sazonais com períodos e fases diferentes.

Espero que estes conceitos tenham te ajudado a entender um pouco mais sobre a previsão em séries temporais. Aqui na Alura, você pode começar os seus estudos sobre o tema no curso Análise de série temporal: COVID-19 e Data Science: análise de séries temporais para previsão.

Modelos matemáticos utilizados em séries temporais

Modelos autorregressivos e de média móvel

Estacionariedade

Facebook Prophet

Cursos