Métricas de avaliação para modelos de regressão
Modelos de regressão estão presentes em inúmeros setores da indústria ou do conhecimento. Eles podem ser utilizados para estimar vendas, mudanças climáticas e até para previsões de desenvolvimentos de doenças.
Para construir o modelo, são observadas correlações entre as variáveis explicativas e a variável resposta do conjunto de dados de interesse e, através de métodos de aprendizado de máquina, é realizado um treinamento. Então, temos um modelo que pode fazer previsões de novos valores.
Mas como garantir que, após o treinamento, o modelo está fazendo um bom trabalho e suas previsões são coerentes?
É aí que entram as métricas de avaliação de modelos de regressão, que ajudam a quantificar o desempenho do modelo e identificar pontos de melhoria.
Neste artigo, vamos explorar algumas métricas básicas, como o R² (Coeficiente de Determinação), até outras mais avançadas e especializadas. Entenderemos quando utilizar cada métrica e quais são suas principais limitações.
Para conhecer algumas métricas importantes que podem ser utilizadas tanto em modelos de regressão simples quanto em séries temporais, recomendo fortemente a leitura do artigo Métricas de avaliação para séries temporais.
O processo de avaliação
Após as etapas de pré-processamento dos dados e divisão em treino e teste, acontece o treinamento propriamente dito.
Porém, esse é um processo iterativo. Parte essencial do treinamento é garantir que o modelo tenha um bom desempenho de previsão ao ser apresentado para novos dados.
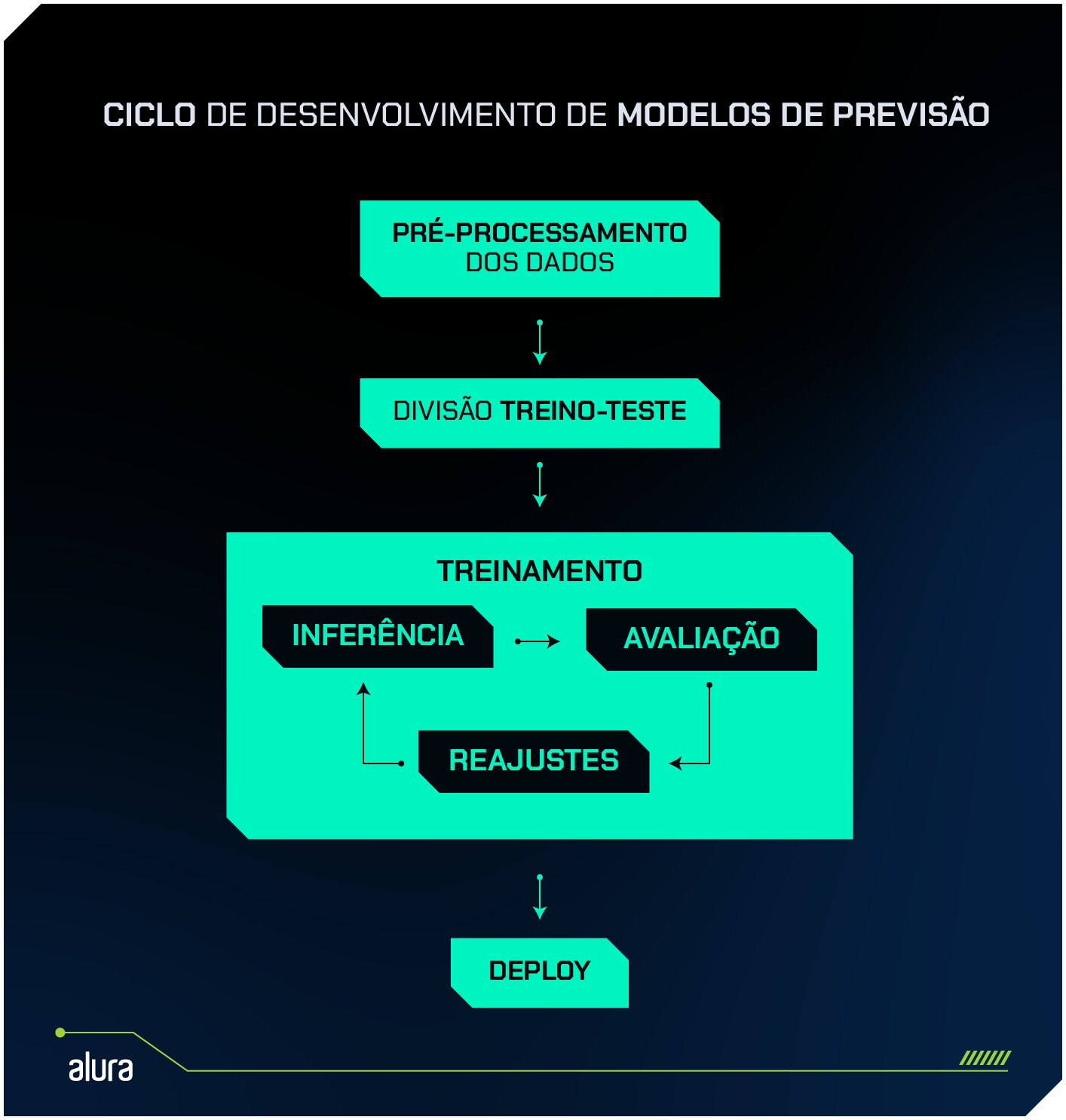
Isso é feito comparando os valores previstos pelo modelo com os valores reais do grupo de teste.
As métricas de avaliação fazem exatamente esse trabalho: elas quantificam o quão próximo o modelo chega dos valores reais, utilizando diferentes cálculos para medir o erro entre as previsões e os resultados já observados.
Cada métrica foca em aspectos diferentes do erro, como a magnitude média do erro (MAE), o desvio em relação à variabilidade dos dados (R²), ou o impacto de grandes desvios (RMSE).
Sendo assim, escolher a métrica certa é fundamental para entender o desempenho real do modelo, além de possibilitar percepções valiosas sobre pontos de melhoria ou ajustes necessários no modelo.

Quais são as métricas de regressão
Agora, vamos explorar algumas das principais métricas utilizadas na avaliação dos modelos de regressão. Apresentarei a fórmula de cada uma e detalhes de sua utilização.
Coeficiente de determinação (R²)
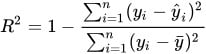
Onde:
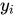
- São os valores reais.
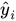
- São os valores previstos pelo modelo.
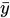
- É a média dos valores reais.
O Coeficiente de Determinação é uma métrica que mede o quanto da variabilidade da variável resposta é explicada pelo modelo. Em outras palavras, ele mostra a proporção da variância dos valores observados que é capturada pelas previsões do modelo.
O valor de R² indica o quanto o modelo se ajustou bem aos dados, onde:
- Quanto mais perto de 1, melhor o modelo explica a variabilidade dos dados;
- Quanto mais perto de 0, pior a qualidade do modelo no ajuste aos dados.
Esse coeficiente se faz especialmente útil em modelos lineares, seja com regressões simples ou múltiplas, e é uma boa métrica inicial para comparar diferentes modelos.
Porém, existem algumas limitações. O R² pode ter resultados enganadores quando existem outliers ou em relações não-lineares entre as variáveis.
Para calcular o R² em Python, você pode utilizar a função r_score da scikit_learn.
from sklearn.metrics import r2_score
# Exemplo de uso:
valores_reais = [10, 15, 20, 25]
valores_previstos = [9, 14, 21, 24]
r2 = r2_score(valores_reais, valores_previstos)
print(f"Coeficiente de determinação (R²): {r2}")
Erro médio absoluto (MAE)
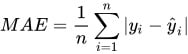
Onde:
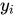
- São os valores reais.
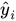
- São os valores previstos pelo modelo.
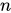
- É o número total de observações.
O erro médio absoluto é uma métrica que indica a magnitude média dos erros em um conjunto de previsões, calculando a média das diferenças absolutas entre os valores reais e os valores previstos pelo modelo.
O MAE é útil para obter uma medida intuitiva do erro médio, sem considerar o sinal (positivo ou negativo), o que facilita a interpretação.
- Quanto menor o valor do MAE, mais próximas as previsões estão dos valores reais.
Uma característica importante do MAE é que grandes desvios não são penalizados de forma desproporcional, então a presença de outliers não tem impacto tão grande no resultado, o que pode ser uma vantagem. Por outro lado, em casos onde o modelo apresenta erros por grandes margens, o resultado do MAE pode não refletir bem o impacto desses desvios.
Para calcular o MAE em Python, você pode utilizar a função mean_absolute_error da scikit-learn.
from sklearn.metrics import mean_absolute_error
# Valores reais e valores previstos (exemplo)
valores_reais = [10, 15, 20, 25]
valores_previstos = [11, 14, 22, 23]
mae = mean_absolute_error(valores_reais, valores_previstos)
print(f"Erro Médio Absoluto (MAE): {mae}")
Embora métricas como MAE e R² forneçam informações valiosas sobre o desempenho geral do modelo, em muitos casos, é necessário utilizar métricas mais sofisticadas para capturar aspectos específicos do erro ou melhorar a precisão em situações mais desafiadoras.
Raiz do Erro Quadrático Médio (RMSE)
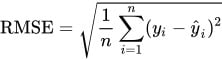
Onde:
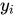
- São os valores reais.
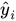
- São os valores previstos pelo modelo.
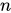
- É o número total de observações.
O RMSE (Root Mean Squared Error) mede o desvio padrão dos erros de previsão, calculando a raiz quadrada da média dos erros quadráticos.
Essa métrica é mais sensível a grandes desvios, pois o erro é elevado ao quadrado, o que significa que grandes diferenças entre o valor previsto e o valor real terão um grande impacto no resultado.
O RMSE é ideal para cenários onde grandes desvios são considerados prejudiciais e devem ser minimizados.
Ele é amplamente utilizado em modelos de séries temporais e em problemas de regressão com distribuições normais.
Sendo assim, o contrário não é tão indicado: devido à penalização excessiva de grandes erros, o RMSE pode não ser adequado para contextos com muitos outliers, onde outras métricas como MAE ou MAPE podem ser mais informativas.
Para calcular o RMSE com Python, utilize a função root_mean_squared_error
from sklearn.metrics import root_mean_squared_error
# Exemplo de valores reais (y_true) e predições (y_pred)
valores_reais = [3, -0.5, 2, 7]
valores_previstos = [2.5, 0.0, 2, 8]
# Calculando o RMSE
rmse_value = root_mean_squared_error(valores_reais, valores_previstos)
print(f"RMSE: {rmse_value:.4f}")
Erro Percentual Absoluto Médio (MAPE)
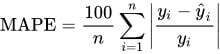
Onde:
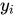
- São os valores reais.
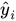
- São os valores previstos pelo modelo.
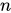
- É o número total de observações.
O MAPE (*Mean Absolute Percentage Error) é uma métrica bastante utilizada para medir o erro médio em termos percentuais.
Por ser uma métrica expressa em porcentagem, tem a vantagem de ser mais facilmente comunicada e compreendida, mesmo em casos de comparações de modelos com escalas muito diferentes.
- Quanto mais baixo o valor do MAPE, melhor o desempenho do modelo;
- Quanto maior o valor do MAPE, mais longe as previsões estão dos valores reais.
Porém, quando os valores observados se aproximam de zero, ou se há recorrência de valores 0, o denominador da equação pode resultar em divisões muito grandes ou indefinidas, o que afeta o cálculo do MAPE.
Outro ponto importante que deve ser considerado é que o MAPE tende a penalizar superestimações de maneira mais severa do que subestimações:
- Superestimação: Quando o valor previsto é maior que o real, o denominador pequeno faz com que a fração do erro seja muito alta, resultando em uma penalização maior.
- Subestimação: Quando o valor previsto é menor que o real, a fração do erro é geralmente menor, já que o denominador (valor real) não é afetado da mesma forma.
Exemplo numérico de penalização assimétrica
Se o valor real for 1 e o valor previsto for 10 (superestimação), o erro percentual será muito grande, pois:
|1 - 10| / 1 = 9
Isso resulta em um erro de 900%.
Agora, se o valor real for 10 e o valor previsto for 1 (subestimação), o erro percentual será:
|10 - 1| / 10 = 0,9
Aqui, o erro percentual é de apenas 90%.
Essa diferença nos valores de erro, dependendo da direção do erro, é o que chamamos de penalização assimétrica no MAPE, já que os erros de superestimação são amplificados enquanto os erros de subestimação são minimizados.
Para calcular o MAPE em Python, você pode utilizar a função mean_absolute_percentage_error do scikit.learn:
from sklearn.metrics import mean_absolute_percentage_error
# Valores reais e valores previstos (exemplo)
valores_reais = [10, 15, 20, 25]
valores_previstos = [9, 14, 21, 24]
# Calculando o MAPE
mape = mean_absolute_percentage_error(valores_reais, valores_previstos)
# Exibindo o resultado em porcentagem
print(f"Erro Percentual Absoluto Médio (MAPE): {mape * 100:.2f}%")
Erro Percentual Absoluto Médio Simétrico (sMAPE)
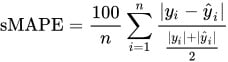
Onde:
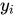
- São os valores reais.
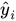
- São os valores previstos pelo modelo.
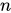
- É o número total de observações.
O sMAPE (Symmetric Mean Absolute Percentage Error) é uma métrica derivada do MAPE (Mean Absolute Percentage Error), projetada para resolver algumas de suas limitações, como a penalização assimétrica de erros de superestimação e subestimação.
A fórmula do sMAPE introduz uma normalização simétrica ao dividir a diferença entre os valores reais e previstos pela média dos valores observados e previstos. Isso equilibra o erro e evita a penalização excessiva de superestimações.
Ainda assim, o sMAPE também apresenta limitações quando os valores observados são muito próximos à zero
A métrica ainda não conta com uma função em biblioteca Python, mas é possível implementar a fórmula:
import numpy as np
def smape(valores_reais, valores_previstos):
# Convertendo para numpy arrays para operações vetoriais
valores_reais = np.array(valores_reais)
valores_previstos = np.array(valores_previstos)
# Fórmula do sMAPE
smape_valor = 100/len(valores_reais) * np.sum(2 * np.abs(valores_previstos - valores_reais) /
(np.abs(valores_reais) + np.abs(valores_previstos)))
return smape_valor
# Exemplo de valores reais e previstos
valores_reais = [10, 15, 20, 25]
valores_previstos = [9, 14, 21, 24]
# Calculando o sMAPE
resultado_smape = smape(valores_reais, valores_previstos)
print(f"sMAPE: {resultado_smape:.2f}%")
Tabelinha com as principais características das métricas citadas
| Métrica | Quando Utilizar | Limitações | Considerações Adicionais |
|---|---|---|---|
| Coeficiente de Determinação (R²) | - Modelos lineares para avaliar o grau de ajuste. - Comparar diferentes modelos. | - Pode dar resultados enganadores em presença de outliers. - Não lida bem com relações não-lineares. | Útil como métrica inicial, mas não indica o erro absoluto ou a escala do erro. |
| Erro Médio Absoluto (MAE) | - Contextos onde é necessária uma medida intuitiva do erro médio. - Quando se quer evitar penalizar grandes erros. | - Não captura o impacto dos grandes desvios. - Insensível à magnitude do erro. | Simples de interpretar, ideal para conjuntos de dados com poucas flutuações bruscas. |
| Raiz do Erro Quadrático Médio (RMSE) | - Quando se deseja dar maior peso a grandes erros. - Modelos com distribuição normal dos erros. | - Penaliza severamente grandes desvios. - Não é robusto contra outliers. | Usado em contextos onde grandes desvios são indesejáveis, como em previsões financeiras. |
| Erro Médio Percentual Absoluto (MAPE) | - Modelos onde a interpretação do erro percentual é mais útil. - Comparação entre diferentes escalas de séries temporais. | - Se valores reais forem zero ou próximos de zero, a métrica se torna instável. | Ideal para comparações entre séries temporais com diferentes magnitudes. |
| Erro Médio Percentual Absoluto Simétrico (sMAPE) | - Modelos onde se deseja equilíbrio entre erros de superestimação e subestimação. - Séries temporais sazonais. | - Instável quando valores reais e previstos são próximos de zero. | Proporciona um erro percentual equilibrado para comparações simétricas. |
Conclusão
Nesse artigo, conhecemos algumas métricas utilizadas para avaliar modelos de regressão.
Descobrimos que a escolha adequada de métricas de avaliação é fundamental, pois só assim é possível garantir que o modelo esteja apresentando um desempenho alinhado às necessidades específicas do problema em questão.
Mesmo quando um modelo se apresenta eficaz no R², ele pode ser insatisfatório quando observamos métricas que penalizam desvios extremos, como é o RSME, por exemplo.
Não existe uma única métrica que atenda todos os cenários de regressão!
É necessário conhecer bem o próprio modelo e as características de cada métrica, com suas limitações e vantagens.
Inclusive, o uso combinado de várias métricas pode trazer um conhecimento mais profundo sobre o desempenho do modelo, além de mapear pontos de melhoria que poderiam estar inicialmente ocultos.