Análise de complexidade de algoritmos: qual é a importância?

Atualmente tem ficado mais visível a necessidade de algoritmos mais eficientes para nossas aplicações, seja pela quantidade de dados processados ou pela necessidade de respostas rápidas. Isso nos leva a um dos principais fundamentos do desenvolvimento de software: a análise da complexidade de algoritmos.

É incrível como as linguagens e plataformas de programação mais modernas se responsabilizam pelo funcionamento dos algoritmos por nós. Ainda assim, é muito importante sabermos o porquê e como o nosso código está funcionando, não acha?

Então vamos a um exemplo prático: Imagine que estamos desenvolvendo uma agenda telefônica e ficamos responsáveis por criar a feature de busca de contatos.

Presumindo que todos os contatos já estejam em ordem alfabética, vamos ao trabalho!

Busca linear

Para facilitar e evitar erros, vamos apenas percorrer a lista em busca de um contato. Vamos supor que foi solicitado o contato da Wanessa:

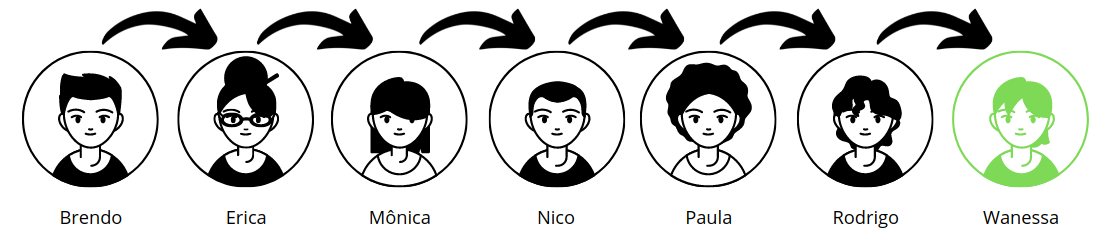
Sequência linear de pessoas com Brendo na primeira posição, Erica na segunda, outras pessoas, Erica na segunda, Mônica na terceira, Nico na quarta, Paula na quinta, Rodrigo na sexta e Wanessa na sétima, destacada das outras pessoas.

Percebemos que percorremos toda a lista até achá-la. Até aqui sem problemas, certo? A solução atual funciona perfeitamente e com um desempenho aceitável. Agora imagine que nossa solução foi vendida para uma empresa multinacional que tenha milhares ou até milhões de contatos.

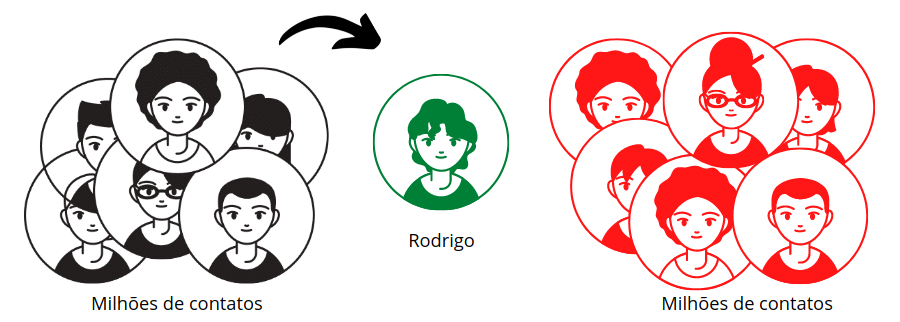
Imagem que representa todo o percurso da busca linear, mostrando a passagem por milhões de contatos até achar o contato do Rodrigo.

Para achar o Rodrigo agora, tivemos que percorrer milhões de contatos! O que não parece ter um bom desempenho, não é?

Busca Binária

Então vamos pensar numa solução melhor. Sabemos que a lista já está em ordem alfabética, então que tal dividi-la? Podemos comparar o contato que procuramos com o contato do meio, verificar a direção que precisamos tomar e eliminar o restante da lista. Portanto, seguiremos os passos descritos para achar o contato da Paula:

Sequência linear de pessoas com Brendo na primeira posição, Erica na segunda posição, Mônica na terceira, Nico na quarta destacado das outras pessoas, Paula na quinta, Rodrigo na sexta e Wanessa na sétima. Uma seta verde apontando para a direita passa por cima dos nomes Nico, Paula e Rodrigo.

Selecionamos o contato do meio, Nico, para comparar com o contato que buscamos, Paula, e descartamos a metade da lista na qual temos certeza que não estará a pessoa procurada.

Sequência linear de pessoas com Paula na primeira posição, Rodrigo na segunda posição e Wanessa na terceira. Uma seta verde apontando para a esquerda passa acima dos nomes de Rodrigo e Paula.

Já nesta iteração, mais uma vez escolhemos o contato do meio da lista, Rodrigo, e verificamos em qual direção temos que ir, descartando a outra metade. Assim achamos Paula.

E qual seria a diferença entre as duas soluções?

Perceba que na primeira solução, independentemente do tamanho da lista, devemos percorrer todos os contatos até acharmos aquele que desejamos. Se tivermos sorte, o contato que procuramos pode ser o primeiro de todos. Porém, se não tivermos essa sorte e procurarmos pelo último contato, teremos que percorrer toda a lista, o que seria o pior caso para o algoritmo. Pensando assim, podemos determinar que nossa primeira solução executa uma função que cresce de forma linear ao tamanho da lista de contatos.

Já na segunda solução, percebemos que a cada iteração eliminamos metade da lista, fazendo com que não seja necessário percorrê-la por completo. Dessa forma otimizamos a busca. Essa solução executa uma função que cresce em taxa logarítmica considerando o tamanho da lista de contatos.

Vamos visualizar a diferença entre as taxas de crescimento de algoritmo?

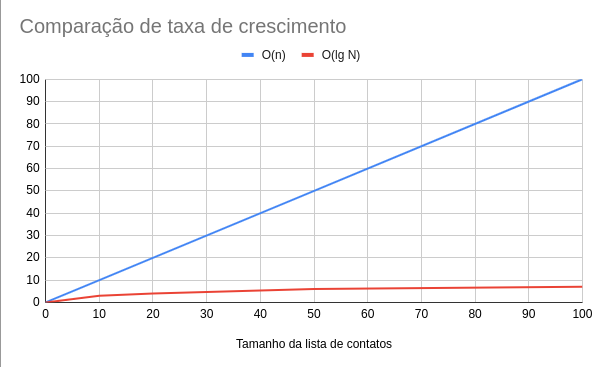
Gráfico que demonstra a comparação entre a busca linear O(n) e a busca binária O(lg N), na busca linear para 100 contatos realizamos 100 comparações no pior caso. Na busca binária para 100 contatos, executamos 7 comparações no pior caso.

Agora fica claro que a solução logarítmica tem um desempenho extremamente mais eficiente que a solução linear, e podemos confirmar através do gráfico acima, onde o eixo da quantidade de operações executadas pelas duas funções é bastante desigual.

Aprofundando mais um pouco, em uma lista com 1 milhão de contatos é necessário realizar apenas 20 operações de comparação até encontrar o contato desejado. Com isso podemos começar a entender o quão importante é a análise da complexidade de algoritmos.

Utilizamos um exemplo bem simples agora, mas imagine ter que desenvolver uma feature de busca de alunos da Alura para que seja possível realizar a autenticação no site ou app. Qual solução você usaria?

Gostou do tema? Temos uma série de novos artigos explicando mais sobre análise da complexidade de algoritmos. Nos próximos abordaremos a implementação dos algoritmos de busca explicados anteriormente.